Deep Residual Learning for Image Recognition

Abstract
由于深度神经网络更难训练。
但网络的层数越多,意味着能够提取到不同level的特征越丰富。并且,越深的网络提取的特征越抽象,越具有语义信息。对于原来的网络,如果简单地增加深度,会导致梯度弥散或梯度爆炸。
于是引入了残差学习框架来简化对于更深网络的训练。同时残差网络更容易被优化以及再增加层数(深度)后得到更好的结果。简单来讲,使用resnet后至少不会让结果更差。
1.Introduction
DNN导致了图像分类得到了巨大的突破,同时神经网路集成了低/中/高级别特征和分类器,且特征的“级别”(包含信息的多少)可以通过堆叠层数(深度)来丰富,所以加深网络的深度十分重要,所以引出了一个问题:”训练更好的网络是否和堆叠更深的层一样容易呢?“,这个问题中很大的阻碍就是梯度消失/爆炸的问题。然而这个问题已经通过归一化初始化(Normalized Initialization)和中间归一化层(Intermediate Normalization Layers)得到了良好的解决使得大概10层的可以通过随机梯度下降(Stochastic Gradient Descent, SGD)和反向传播(Backpropagation)得到收敛。
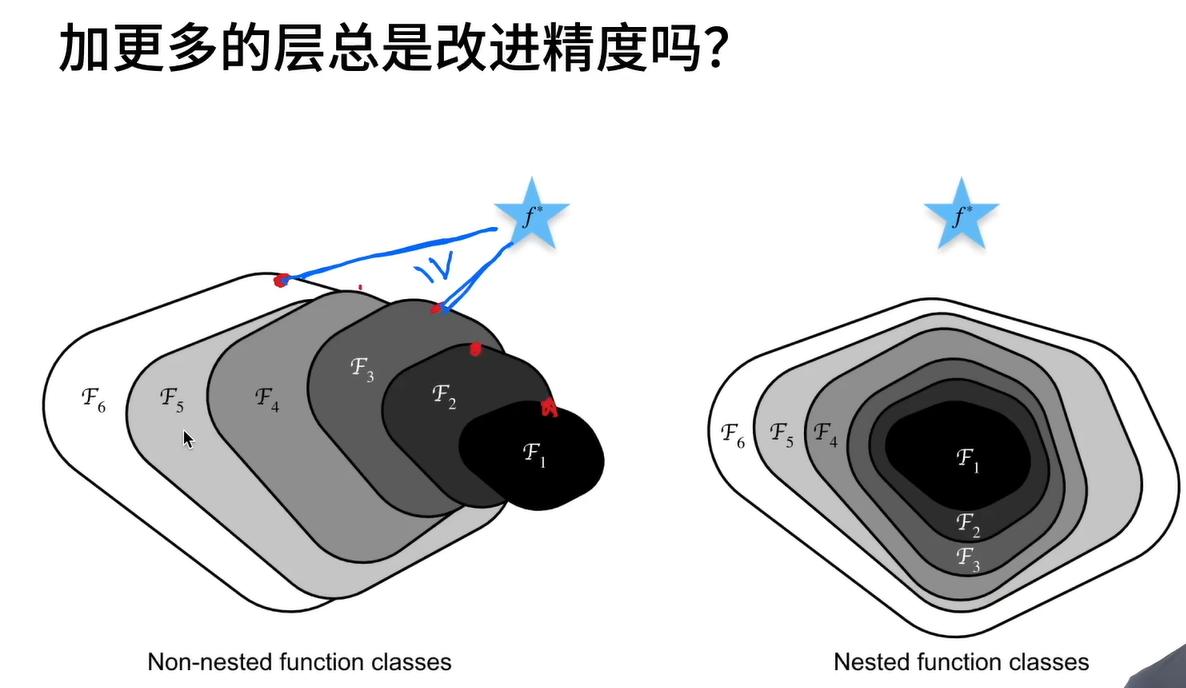
当更深的网络开始收敛时,一个退化问题就暴漏出来:随着网络深度的增加,准确度变得饱和,然后迅速退化。然后这种退化不是由过拟合(overfitting)导致的。
于是残差网络被提出,它实现了恒等映射(identity mapping),允许输入直接跳过这些层并加到输出上。
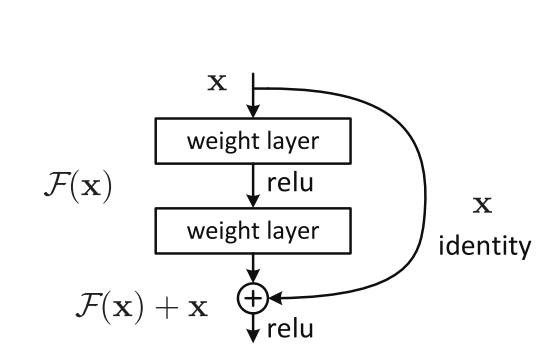
F(x)+x的公式可以通过具有“快捷连接”(shortcut connection)的前馈神经网络来实现。其中快捷连接指代的是跳过一个或多个层的连接。例如下图中identity部分,其中快捷连接只是执行恒等映射,并将输出添加到了堆叠层的输出中。恒等快捷连接既不增加额外的参数也不增加复杂度。
3.Deep Residual Learning
残差函数
传统的神经网络层直接通过输入x得到目标映射H(x),而残差网络提出让网络层学习残差映射,即输入为:
这样输出就为:
其中F(x)为残差函数,这种设计通过Shortcut Connection(跳跃连接)将输入直接传递到输出层,使得网络能够更轻松地学习输入与输出之间的差异,而非完整的映射。因将原始的信息Xi直接传递给了X(i+1)从而避免了信息损失。
在这里对于为何叫残差网络进行解释:
虽然看着是从原来输出F(x)变为了输出(H(x))F(x)+x好似进行了加法操作,但实际上这里的残差指代着是输出相对于输入的差值,即F(x)= H(x) -x。关键在于网络不再直接拟合目标映射 H(x),而是将其分解为 H(x)=F(x)+x 的形式,其中 F(x) 就是“残差”函数,即需学习的部分 F(x)=H(x)-x。这样做的优点在于:当理想映射接近恒等映射(H(x)= x)时,只需让 F(x)=0,优化器更容易收敛。
残差块

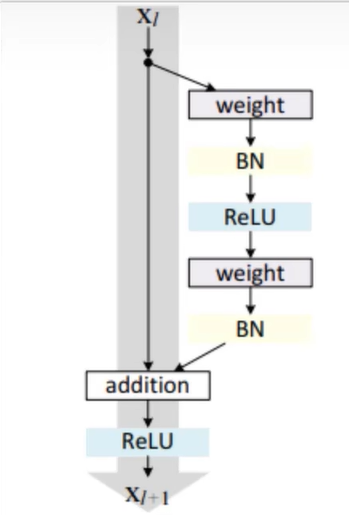
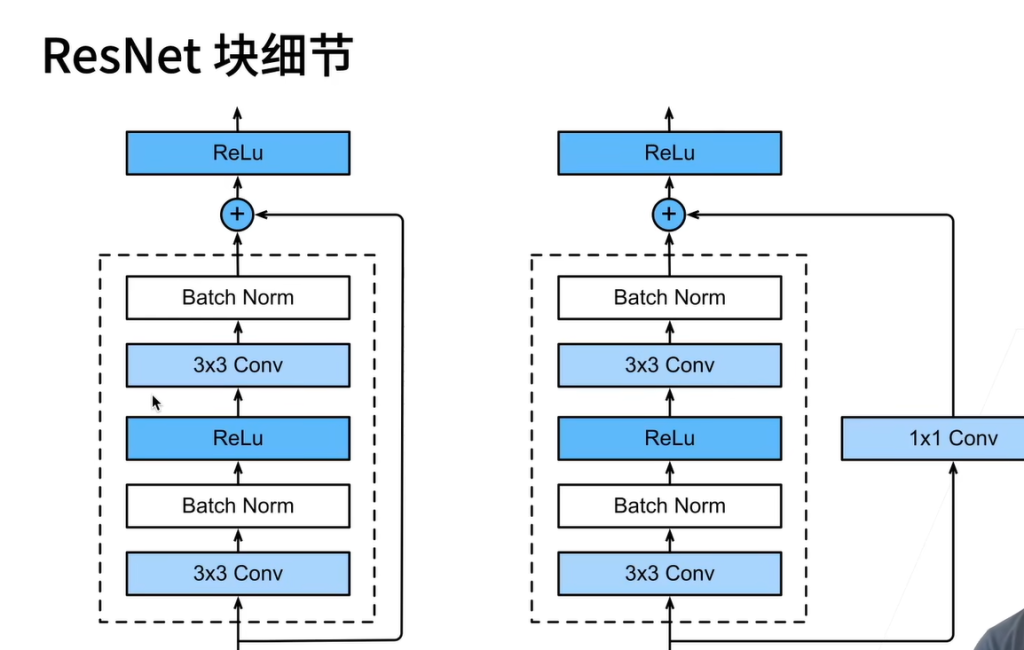
def res_block_v1(x, input_filter, output_filter):
res_x = Conv2D(kernel_size=(3,3), filters=output_filter, strides=1, padding='same')(x)
res_x = BatchNormalization()(res_x)
res_x = Activation('relu')(res_x)
res_x = Conv2D(kernel_size=(3,3), filters=output_filter, strides=1, padding='same')(res_x)
res_x = BatchNormalization()(res_x)
if input_filter == output_filter:
identity = x
else: #需要升维或者降维
identity = Conv2D(kernel_size=(1,1), filters=output_filter, strides=1, padding='same')(x)
x = keras.layers.add([identity, res_x])
output = Activation('relu')(x)
return output
1×1 卷积核的大小是 1×1×input_filter×output_filter,其中 input_filter 是输入的通道数,output_filter 是输出的通道数。
ResNet架构
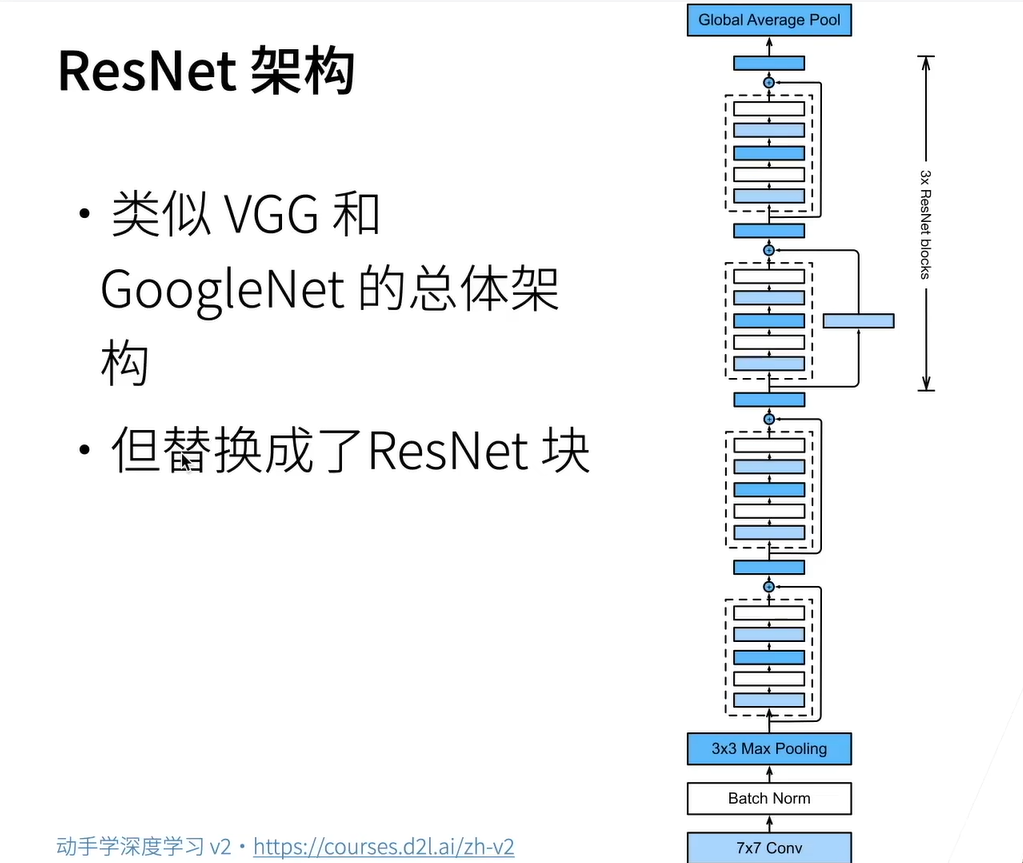
ResNet : Residual Network(残差网络)
残差连接如何处理输入输出不等的情况:
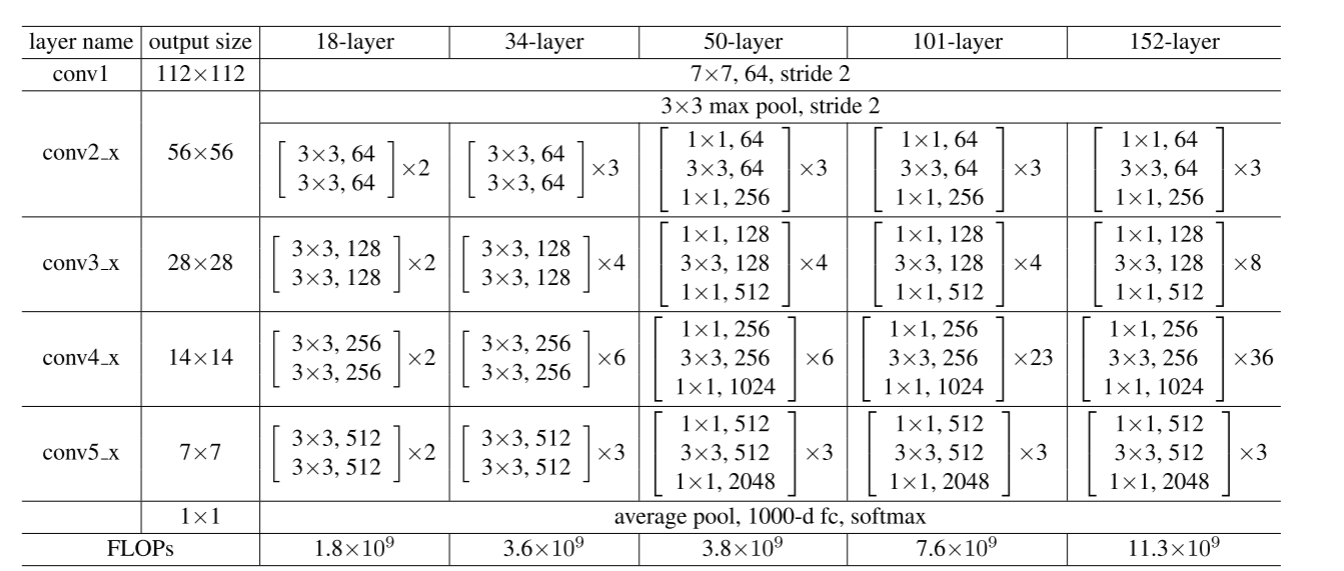
其中layer name中的x表示里面有很多不同的层(块)
FLOPs:表示网络需要计算多少浮点运算
FLOPs=(卷积核长卷积核宽输入通道数输出通道窗口的高窗口的宽全连接
对于34-layer来讲,第一个块中:
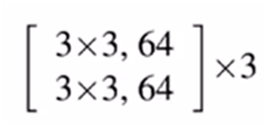
组成为3*3,通道数为64,一共有3个这样的块(相当于复制多少次),块之间通过残差连接(residual connection)来连接的,具体实现如下图:
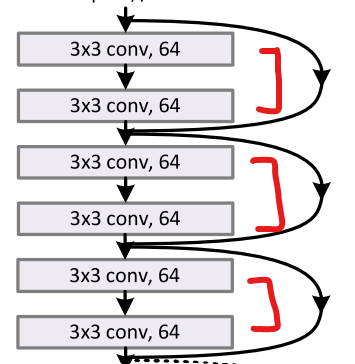
34-layer的统计下来一共34层(3+4+6+3)*2+1(conv1层)+1(最后一个全连接层)
统计层数只统计带有训练参数的层,包括卷积层 ,全连接层,不算池化层和BN层
池化没有权重参数,没有参数的层,通常不算。池化操作只是降数据量,并没增加模型参数

